SIFT
What is SIFT(Scale-invariant Feature Transform)
SIFT,它既是一个 Detector,又是一个 Descriptor。SIFT具有尺度不变性、旋转不变性、光照不变性和视角不变性。那么我们为什么需要这些性质呢?
显然,这些性质是有实际需求的。以尺度不变性为例,当我们在使用 Harris 算子做角点检测时,我们所划定的区域大小直接决定了我们是否能提取到我们所需要的角点。如下图所示,当我们选择的区域大小不同时(图中表示为方块的面积大小),我们所得到的检测结果显然是不同的。当选择图片左侧所示方块大小时,我们看到的是一个角,而如果选择右侧所示方块大小时,我们所检测到的则是边界。可以想象,如果把左侧区域继续放大,那我们最终检测到的将是一个平面。
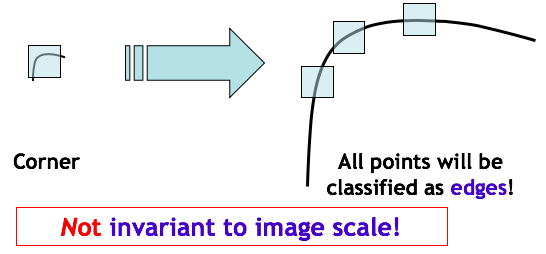
由此,我们希望能够有一个算法,它能够帮助我们准确地识别出来到底是 edge 还是 corner 亦或者是 flat。
SIFT 算法步骤
1. 构建尺度空间
可以说这个SIFT里面最简单的一步了。Scale Space,尺度空间,实际上是指使用不同参数 \(\sigma\) 的高斯核对同一张图片做卷积运算后得到的图片序列。使用高斯核做卷积运算也可称为对图像进行高斯模糊。经过高斯模糊之后的图像可表示为:
\[ L(x,y,\sigma)=G(x,y,\sigma)*I(x,y) \]
其中高斯核为: \[ G(x,y,\sigma)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}} \]
为了得到尺度空间,我们选用不同的\(\sigma\)来得到一组图片,这一组图片中依次是使用原图像和参数分别为\((\sigma, k\sigma, k^2\sigma, k^3\sigma, \cdots)\)进行高斯模糊,我们可以使用\(k = \sqrt{2}\)作为倍数。这一组图片我们称为一个 Octave,每个 Octave中有多张图片。我们需要构建多个Octave,每个Octave中图像的大小都是前一组的一半。

2. DoG(Difference of Gaussian)与 LoG(Laplacian of Gaussian)
首先我们来看下什么是LoG。LoG就是对高斯核计算二阶导。
\[ \begin{align*} \alpha&=\frac{1}{\sqrt{2\pi\sigma^2}}\\ \frac{\partial^2}{\partial^2x}G_{\sigma}(x,y)&=\alpha\frac{x^2-\sigma^2}{\sigma^4}e^{-\frac{x^2+y^2}{2\sigma^2}}\\ \frac{\partial^2}{\partial^2y}G_{\sigma}(x,y)&=\alpha\frac{y^2-\sigma^2}{\sigma^4}e^{-\frac{x^2+y^2}{2\sigma^2}}\\ LoG&=\frac{\partial^2}{\partial^2x}G_{\sigma}(x,y)+\frac{\partial^2}{\partial^2y}G_{\sigma}(x,y)\\ &=\alpha\frac{x^2 + y^2-\sigma^2}{\sigma^4}e^{-\frac{x^2+y^2}{2\sigma^2}} \end{align*} \]
虽然LoG可以很好的完成边缘检测的任务,但是他最大的缺点就是计算复杂度非常的高。这就需要寻找一种近似方法来提高效率。而这个方法就是DoG。
假设我们现在有两张使用不同参数\(\sigma\)做高斯模糊后的图像,即 \[
g_1(x,y) = G(x,y,\sigma_1) I(x,y)\\
g_2(x,y) = G(x,y,\sigma_2) I(x,y)\\
\] 将两幅图像相减之后即得到DOG得到 \[
\begin{align*}
DoG=
g_1(x,y)-g_2(x,y)
&= G(x,y,\sigma_1)*I(x,y) - G(x,y,\sigma_2)*I(x,y)\\
&= \left(G(x,y,\sigma_1) - G(x,y,\sigma_2)\right)*I(x,y)
\end{align*}
\] 这时的DoG已经具有了尺度不变性。
3. 寻找关键点
要找到关键点,我们只需要找出一个空间最大值即可。

在一个octave中,我们选择一张图片A,图片A前一张图片为B,后一张图片为C,我们选择A中的一个像素,比较A周围8个像素,B中A对应位置以及其周围8个像素,C中A对应位置以及其周围的8个像素,总计8+9+9=26个像素(上图中X即为所选像素,绿色点代表上述26个像素),如果我们所选的像素是这其中最大或者最小的,那么这个点就是 Interest Point or Keypoint。
然而,仅仅找到这些关键点是不够的,我们还需要对他们进行筛选。筛选的原则就是我们希望最后得到的关键点是能让DoG最大化的点。这里就需要用到对离散函数的泰勒展开式。
对一个多元函数,其泰勒展开式可表示为 \[ D(x) = D+\frac{\partial D^T}{\partial x}\Delta x+\frac{1}{2}\Delta x^T\frac{\partial^2 D^T}{\partial x^2}\Delta x \] 为求极值点,令上式导数为0,得到 \[ \Delta x=-\frac{\partial D^{-1}}{\partial x^2}\frac{\partial D}{\partial x} \] 代入后得到 \[ D(\hat{x})=D+\frac{1}{2}\frac{\partial D^T}{\partial x}\hat{x} \] 对于筛选过程,一共分为2步
- 如果\(D(\hat{x}) < 0.03\),则剔除这个点
- 检测关键点DoG函数的曲率?
4. 寻找主方向
目前,我们已经得到了关键点的坐标\((x,y)\)以及所对应的尺度\(\sigma\),那么我们可以根据这些信息,选择尺度最接近\(\sigma\)的高斯模糊后的图像,计算\(2*3*\sigma\)邻域中像素点的HoG,邻域中的每个点的权重根据高斯核给出。得到HoG之后,峰值所对应的\(\theta\)作为主方向。如果存在另一个方向\(\theta^{\prime}\),其对应的直方图高度为主方向对应高度的80%,那么就选为辅方向(有时还要求这个辅方向是局部最大值,即比他相邻的两个方向所对应高度更高)。
由此,我们得到了关键点的一个描述,即\((x,y,\sigma,\theta)\)。一个关键点只能有一个主方向,辅方向可以有多个,使用时我们仅仅简单的复制这些点的描述。例如\((x,y,\sigma,\theta), (x,y,\sigma,\theta_1), (x,y,\sigma,\theta_2) \cdots\)。
5. 生成特征描述
对关键点附近的\(16*16\)的邻域,切分成16个\(4*4\)的小方格,对每个小方格做HoG,并使用基于关键点距离的高斯权重函数对每个点的权重做出调整。最后将16个8维特征组合起来,形成SIFT Descriptor
Reference
- Laplacian of Gaussian
- Difference of Gaussian
- 离散函数的泰勒展开